Saturated Fatty Acids and Methyl Esters

¹H-NMR Spectroscopy of Fatty Acids and Their Derivatives

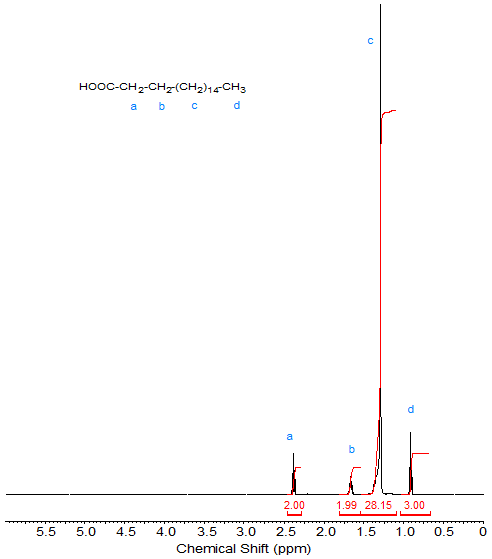
As mentioned in the Introduction to these web pages, because of their relative simplicity, the NMR spectra of stearic acid and methyl stearate will serve as references when discussing the "introduction" of other functional groups. The ¹H-NMR spectrum (see Fig. 1) of stearic acid shows the following peaks:

• 2.35 ppm: CH₂ α to COOH (C2 methylene; triplet);
• 1.65 ppm: CH₂ of C3; multiplet
• 1.3-1.4 ppm: CH₂ of C3-C16; theoretical integration value 28 (note the deviation in Fig. 1; this deviation is especially noticeable for the large number of CH₂ protons in a long chain when assigning each proton an integration value of 1).
• 0.88 ppm: CH₃ (C18 terminal methyl; triplet).

The proton of the carboxylic acid group is beyond the spectral range shown here (see Table 1 in the Introduction).

Figure 1. ¹H-NMR spectrum of stearic acid.

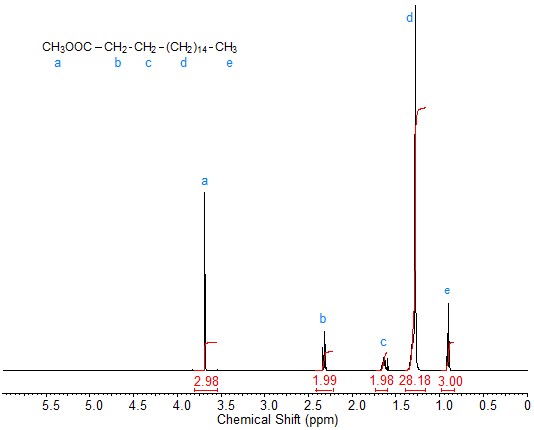
The ¹H-NMR spectrum of methyl stearate (Fig. 2) is virtually identical to that of stearic acid except for the strong singlet peak caused by the methyl ester protons at about 3.7 ppm. This peak of the methyl ester protons can be useful for quantification purposes when monitoring reactions such as transesterification.

Figure 2. ¹H-NMR spectrum of methyl stearate.

Obviously, in the spectra of other saturated fatty acids and methyl esters, the intensity and the integration value of the signals of the methylene moieties change. With the change in integration value, and if the integration is sufficiently accurate, fatty acid chain length can be determined, although this is of little practical value.